考研高数公式总结

本网页主要是作为听课笔记，部分内容是经过本人理解加工后记录的，由于本人水平有限，可能有一些有误的地方，敬请谅解。

第1章 极限与连续

函数性质

有界性：①有界*有界=有界②无界*无界→不一定是无界③有界*无界→不一定是无界

④A*B为无界→A或B为无界 ⑤A*B有界→A、B不一定有界

极限定义:对于任意ε＞0,存在N＞0,当n＞N时,有|a_n-A|＜ε,则称A为数列{a_n}的极限,记为

极限性质

函数极限正(负), 则去心领域正(负);

函数不正(负),极限不正(负);

等价无穷小

α~β的充要条件:β=α+o(α)

代换条件：乘除可以换、加减在满足精度（同阶）的前提下可以换，判断法如下所示

两个重要极限

不定型

0/0型计算 1）洛必达法则 2）等价无穷小代换 3）泰勒

1^∞型计算

无穷小的比较

泰勒公式

阶数的确定方法：将目标式泰勒展开后的第一个不为零的项的次数

若原函数难算，可以先求导，将求导结果泰勒展开后再积分

连续和间断

1.连续:f(x)在点x=a处连续的充要条件:f(a-0)=f(a)=f(a+0) 左极限=右极限=函数值

2.间断

①第一类间断点:f(a-0)和f(a+0)存在

可去间断点:f(a-0)=f(a+0)(≠f(a) )

跳跃间断点:f(a-0)≠f(a+0)

②第二类间断点:f(a-0)和f(a+0)至少有一个不存在

题型总结

第2章 导数与积分

基本概念

导数定义

可导的条件：左导数f_-^'(x₀)=右导数f₊^'(x₀)

常见概念

可导一定连续，连续不一定可导

函数和其导函数奇偶性相反

导数、微分公式

隐函数、参数方程确定的函数求导

第3章 一元函数微分学的应用

中值定理

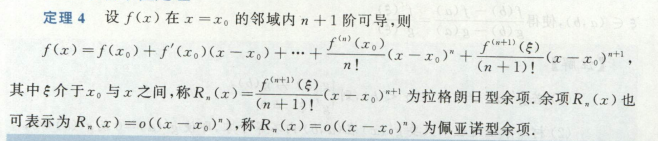
第4章 不定积分

第5章 定积分及其应用

广义积分

第6章 多元函数微分学

二元函数可微判别法

Δz=AΔx+BΔy+o(ρ)    A是z对x的偏导，B是z对y的偏导

方法：看Δz-AΔx-BΔy是否是ρ的高阶无穷小

类比一元函数微分定义Δy=AΔx+o(x)    A是y对x的导数