人工智能导论 知识点总结

第1章 概述

人工智能定义：人工智能亦称机器智能，是指由人制造出来的机器所表现出来的智能。通常人工智能是指通过普通计算机程序的手段实现的类人智能技术。

三大学派：符号学派、连接学派、行为学派

从智能角度对人工智能的分类：

（1）（传统）专用人工智能:依葫芦画瓢、任务导向

（2）通用人工智能（跨领域人工智能）:举一反三、从经验中学习

三种主流方法

第2章 逻辑与推理

2.1命题逻辑

命题逻辑：应用一套形式化规则对以符号表示的描述性陈述进行推理的系统。

原子命题（简单命题）：不包含其他命题作为其组成部分的命题。

复合命题：若干原子命题可通过逻辑运算符来构成复合命题。

命题联结词

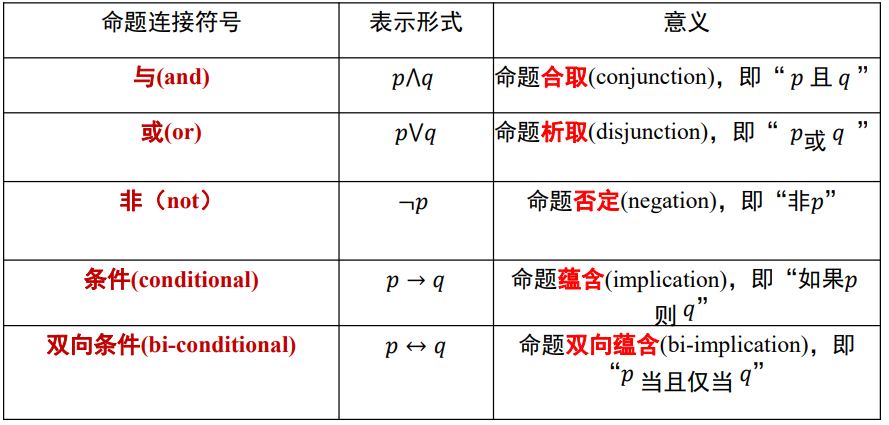
蕴涵关系：如果𝑝那么𝑞(𝑝 ⟶ 𝑞)（充分条件），命题q包含命题p（p是q的子集），若P不成立相当于P是空集，空集是任何集合的子集。

逻辑等价

逻辑等价：𝑝 ≡ q

推理规则

鲁滨逊归结原理（消解原理）：检查子句集 S 中是否包含空子句，若包含，则 S 不可满足。若不包含，在 S 中选择合适的子句进行归结，一旦归结出空子句，就说明 S 是不可满足的。

一般将所证结论取反（作为条件之一），推出空语句，从而取反的结论不成立，那么所证结论成立。

附加律：A ⇒ ( A ∨ B ) （如果A是对的，那么A ∨ B 也是对的）

化简律：( A ∧ B ) ⇒ A , ( A ∧ B ) ⇒ B

假言推理：(A→B)∧A⇒B

拒取式：( A → B ) ∧ ¬ B ⇒ ¬ A

析取三段论：( A ∨ B ) ∧¬A ⇒ B , ( A ∨ B ) ∧ ¬ B ⇒ A

( A ∨ B )是正确的 , 其中A是错误的 , 那么B肯定是正确的 ;

( A ∨ B )是正确的 , 其中B是错误的 , 那么A肯定是正确的 ;
假言三段论：( A → B )∧( B → C )⇒( A → C )

等价三段论：(A ↔ B )∧( B ↔ C )⇒( A ↔ C )

构造性两难：( A → B )∧( C → D )∧( A ∨ C )⇒( B ∨ D )

命题范式

⚫ 析取范式：有限个简单合取式构成的析取式称为析取范式 例𝛼 = 𝛼1 ∨ 𝛼2 ∨ ⋯ ∨ 𝛼k

⚫ 合取范式：有限个简单析取式构成的合取式称为合取范式 例𝛼 = 𝛼1 ∧ 𝛼2 ∧ ⋯ ∧ 𝛼k

*命题公式的析取范式与合取范式都不是唯一的

2.2 谓词逻辑与推理

⚫ 个体：个体的取值范围为个体域，个体可以是常量、变元或函数。谓词中可以有若干个个体变量

⚫ 谓词：用来刻画个体属性或者描述个体间关系存在性的元素，其值为真或假

*函数是从定义域到值域的映射；谓词是从定义域到{𝑇𝑟𝑢𝑒, 𝐹𝑎𝑙𝑠𝑒} 的映射

⚫ 量词：①全称量词：表示全体的 符号：∀ ②存在量词 表示存在 符号：∃

约束变元：受量词约束的变量符号 自由变元：不受量词约束的变量符号

合式公式（谓词公式）：由逻辑联结词和原子公式构成，在合式公式中，连接词之间的优先级别是 ┓，∧，∨，→， ←→

谓词逻辑的推理规则：

⚫ 全称量词消去: (∀𝑥)𝐴(𝑥 )→ 𝐴(𝑦)
⚫ 全称量词引入: 𝐴(𝑦) → (∀𝑥)𝐴 𝑥
⚫ 存在量词消去: (∃𝑥)𝐴(𝑥) → 𝐴(𝑐)
⚫ 存在量词引入: 𝐴(c) → (∃𝑥)𝐴(𝑥）

2.3 知识表示与知识图谱

知识表示 知识的要素
• 事实：事物的分类、属性、事物间关系、科学事实、客观事实等。（最低层的知识）

• 规则：事物的行动、动作和联系的因果关系知识。（启发式规则）。
• 控制：当有多个动作同时被激活时，选择哪一个动作来执行的知识。（技巧性）
• 元知识：高层知识。怎样实用规则、解释规则、校验规则、解释程序结构等知识。

知识图谱

知识图谱由有向图构成。在图中，每个节点是一个实体（如人名、地名、事件和活动等），任意两个节点之间的边表示这两个节点之间存在的关系。

知识图谱推理 (inference) ：通过机器学习等方法对知识图谱所蕴含关系进行挖掘。

知识图谱中任意两个相连节点及其 连 接 边 表 示 成 一 个 三 元 组 （ triplet ） ， 即(left_node, relation, right_node) 这种三元组也可以表示为一阶逻辑(first order logic, FOL)的形式，从而为基于知识图谱的推理创造了条件

例如从<奥巴马，出生地，夏威夷>和<夏 威夷，属于，美国>两个三元组，可推理 得到<奥巴马，国籍，美国>

• 概念：层次化组织
• 实体：概念的示例化描述
• 属性：对概念或实体的描述信息
• 关系：概念或实体之间的关联
• 推理规则：可产生语义网络中上述新的元素

知识图谱推理：FOIL (First Order Inductive Learner)

正例+反例+背景知识⟹ 假设 （反例： 可从知识图谱中构造出来 背景知识：知识图谱中目标谓词以外的其他谓词实例化结果）

前提约束谓词 (学习得到)⟹ 目标谓词 (已知)

推理思路：从一般到特殊，逐步给目标谓词添加前提约束谓词，直到所构成的推理规则不覆盖任何反例。

依次将其它谓词（背景知识）加入到推理规则中作为前提约束谓词， 并计算所得到新推理规则的FOIL增益值。 基于计算所得FOIL增益值来选择最佳前提约束谓词。直到推理规则不覆盖任何反例（将信息增益最大的加入推理规则，将训练样例中与该推理规则不符的样例去掉）

给定目标谓词，FOIL算法从实例（正例、反 例、背景样例）出发，不断测试所得到推理规 则是否还包含反例，一旦不包含负例，则学习 结束，展示了 “归纳学习”能力。

2.4因果推理

辛普森悖论表明，在某些情况下，忽略潜在的“第三个变量”，可能会改变已有的结论

用来进行因果推理的模型：结构因果模型（因果模型）、因果图、贝叶斯网络

结构因果模型：由两组变量集合U和V以及一组函数f组成。（f是根据模型中其他变量而给V中每一个变量赋值的函数）

每个结构因果模型𝑀都与一个因果图𝐺相对应

有向无环图

有向无环图(DAG)：有向无环图指的是一个无回路的有向图，即从图中任意一个节点出发经过任意条边，均无法回到该节点。有向无环图刻画了图中所有节点之间的依赖关系。DAG 可用于描述数据的生成机制。这样描述变量联合分布或者数据生成机制的模型，被称为 “贝叶斯网络”（Bayesian network）。

一个有向无环图唯一地决定了一个联合分布；反过来，一个联合分布不能唯一地决定有
向无环图。反过来的结论不成立。如联合分布𝑃(𝑋1, 𝑋2)= 𝑃(𝑥1)𝑃(𝑥2|𝑥1)=𝑃(𝑥2)𝑃(𝑥1|𝑥2)

𝐷-分离

𝐷-分离用于判断集合𝐴中变量是否与集合𝐵中变量相互独立（给定集合𝐶），
记为 𝐴 ⊥ 𝐵 | C

A是因 B是果 C是隐藏条件（类似辛普森悖论）

对于一个DAG图，如果𝐴、𝐵、𝐶是三个集合（可以是单独的节点或者是节点的集合），为了判断𝐴和𝐵 是否是 𝐶 条件独立的， 在DAG图中考虑所有𝐴和𝐵之间的路径(不管方向)。对于其中的一条路径，如果满足以下两个条件中的任意一条，则称这条路径是阻塞（block）的：

1. 路径中存在某个节点𝑋是链结构𝐴 → 𝐶 → 𝐵或分连结构𝐴 ← 𝐶 → 𝐵中的节点、 且𝑋包含
   在𝐶中
2. 或者路径中存在某个节点𝑋是汇连结构𝐴 → 𝐶 ← 𝐵中节点，并且𝑋或𝑋 后代不包含在 C
   中

如果𝑨和𝑩 之间所有路径都是阻塞的，那么𝑨和𝑩 就是关于 𝑪 条件独立的；否则𝑨和𝑩不是关于 C 条件独立

有向连接：两个节点间存在一条路径将这两个节点连通

有向分离：不存在这样的路径将这两个节点连通

第3章 搜索求解

3.1基本概念

一个搜索的问题通常包括如下的信息：状态空间、后继函数、起始状态和终点检测

搜索中需要解决的基本问题：
（1）是否一定能找到一个解。
（2）找到的解是否是最佳解。
（3）时间与空间复杂性如何。
（4）是否终止运行或是否会陷入一个死循环。

•状态空间：利用状态变量和操作符号，表示系统或问题的有关知识的符号体系，状态空间是一个四元组：

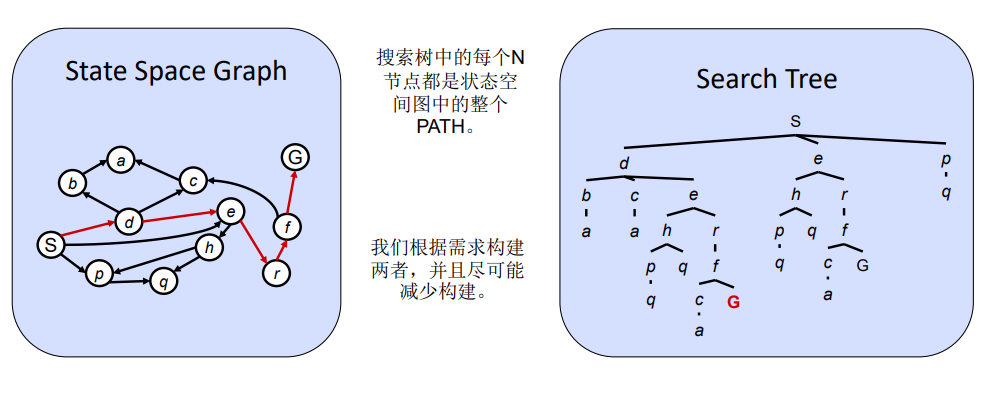
状态图：

在状态空间图中，每个状态仅发生一次

我们很少会在内存中建立完整的图表（太大），但这是一个有用的想法

搜索树

树上反映的是可能的行动规划及其结果
• 开始的状态是根节点
• 子节点反映的是可能的动作结果
• 节点代表状态，但一个状态可能出现多次，反映的是不同行动规划的结果
• 对大多数问题，我们实际上很难建立整个搜索树

3.2盲目式搜索

在不具有对特定问题的任何有关信息的条件下，按固定的步骤（依次或随机调用操作算子）进行的搜索。

搜索树搜索
• 扩展树节点(寻找潜在的行动规划)
• 从搜素前沿（当前的所有叶节点）中考虑扩展：前沿代表了当前所有的规划部分
• 树节点扩展的越少越好

通用的数搜索伪码

关键元素:
• 搜索前沿
• 扩展操作
• 探索（选择）策略
主要问题：从哪些前沿叶节点开始搜索扩展

深度优先搜索(DFS)

策略：优先扩展一个最深的节点（若无解返回到上一个节点，然后从另一条路开始走到底）
实现：前沿是一个后进先出的栈

搜索树:b ：最大分支数 • m ：最大深度 • 解可能存在于不同深度

广度优先搜索（BFS)

策略：优先扩展最浅的节点
实现：前沿是一个先进先出的队列

基于成本的统一搜索

策略：（先进行广度搜索，在结果选择成本低的节点再做广度搜索，若无解返回到上一个节点，选择排除该节点后成本最低的节点进行扩展）扩展一个成本最低的节点
前沿用优先级队列存储（优先级：累计成本）

3.3启发式搜索

启发式策略：利用与问题有关的启发信息进行搜索。

评价函数 ：从初始结点经过结点n到达目的结点的路径的最小代价估计值，其一般形式是

f(n)=g(n)+h(n)

g(𝑛)表示从起始节点到节点𝑛的开销代价值

ℎ(𝑛)表示从节点𝑛到目标节点路径中所估算的最小开销代价值（启发函数）

一般地，在f(n)中，g(𝑛)的比重越大，越倾向于宽度优先搜索方式，而ℎ(𝑛)的比重越大，表示启发性能越强

评价函数的作用：从当前节点出发来选择后续节点

贪婪最佳优先搜索

只扩展当前代价f(n)最小的节点

评价函数f(n)=h(n) 不考虑之前的开销

缺点：

①贪婪最佳优先搜索不是最优的

②启发函数代价最小化这一目标会对错误的起点比较敏感

③贪婪最佳优先搜索也是不完备的。

④最坏的情况下，贪婪最佳优先搜索的时间复杂度和空间复杂度都是O(𝑏𝑚)，𝑏：节点的分支因子数目、𝑚：搜索空间的最大深度。

A*算法

结合统一搜索结合贪婪搜索

• 统一： 把路径成本排序，即来程的成本g(n)
• 贪婪： 排序按照与目标的临近性，即前程成本h(n)

为了保证A*算法是最优 (optimal) ，需要启发函数ℎ(𝑛)是可接受的和一致的(或者也称单调性)。

最优：不存在另外一个解法能得到比A*算法所求得解法具有更小开销代价。

完备：即它不会沿着一条无限的路径走下去而不回来做其他的选择尝试，可以找到最佳路径这一答案。

可接受的（可容性）：专门针对启发函数而言，即启发函数不会过高估计从节点𝑛到目标结点之间的实际开销代价（即小于等于实际开销）。如可将两点之间的直线距离作为启发函数，从而保证其可接受。

一致的(单调性):假设节点𝑛的后续节点是𝑛′，则从𝑛到目标节点之间的开销代价一定小于从𝑛到𝑛′的开销再加上从𝑛′到目标节点之间的开销，即ℎ(𝑛) ≤ 𝑐(𝑛, 𝑎, 𝑛′) + ℎ(𝑛′) 。这里𝑛′是𝑛经过行动𝑎所抵达的后续节点， 𝑐(𝑛, 𝑎, 𝑛′) 指𝑛′和𝑛之间的开销代价。

• 如果函数满足一致性条件，则一定满足可接受条件；反之不然。
• 直线最短距离函数既是可接受的，也是一致的。

如果A*算法将节点n选择作为具有最小代价开销的路径中一个节点，则𝑛一定是最优路径中的一个节点。即最先被选中扩展的节点在最优路径中。

Tree-search 树搜索

Tree-search 完成一次扩展和前沿中的其它节点对比 始终选择最小的进行扩展 没有检测重复出现的状态，导致产生节点成树深度的指数增长。

Tree-search的A*算法中，如果启发函数ℎ(𝑛) 是可接受的，则A*算法是最优的和完备的；

Graph-search 图搜索

在Graph-search的A*算法中，如果启发函数ℎ(𝑛) 是一致的，A*算法是最优的。

3.4对抗搜索

最小最大搜索(Minimax Search):

给定一个游戏搜索树(max层和min层交替），minimax算法计算每个节点的minimax值来决定最优策略，MAX希望最大化minimax值(在max层选择最大值），而MIN则相反

该算法需要遍历所有的节点

性能：（b宽度 m深度）
• 时间: O(b^m)
• 空间: O(bm)

优点:
算法是一种简单有效的对抗搜索手段

在对手也“尽力而为”前提下，算法可返回最优结果
缺点:
如果搜索树极大，则无法在有效时间内返回结果
改善:
使用alpha-beta pruning算法来减少搜索节点

对节点进行采样、而非逐一搜索 (i.e.,MCTS)

Alpha-Beta 剪枝搜索

max 方节点的当前最优值被称为α值（初始值：-∞），min 方节点的当前最优值被称为β 值（初始值：+∞）。在搜索过程中，max 节点使α 值递增，min 节点则使 β值递减，两者构成一个区间[ α ，β] ，这个区间被称为窗口。窗口的大小表示当前节点值得搜索的子节点的价值取值范围，向下搜索的过程就是缩小窗口的过程，最终的最优值将落在这个窗口中。

每个节点有两个值，分别是𝛼和𝛽。节点的𝛼和𝛽值在搜索过程中不断变化。其中，𝛼从负无穷大(−∞)逐渐增加、𝛽从正无穷大(∞)逐渐减少。如果一个节点中𝛼 > 𝛽，则该节点的后续节点可剪枝。

剪枝在大多数情况下会提高算法效率

第4章 监督学习

4.1机器学习

特征：是输入变量，“学习” 问题通常包括n个样本数据（训练样本），然后预测未知数据（测试样本）属性每个样本包含的多个属性（多维数据）。

标签：对事物的凭经验的分类。

样本：是指数据的特定实例。

机器学习：从原始数据中提取特征，学习一个映射函数f将特征映射到语义空间，寻找数据和任务目标间的关系。（是研究算法的过程，是用数据或经验E，研究在某些任务T中提高性能P的算法。）

监督学习的重要元素

模型：定义了特征与标签之间的关系

4.1.2机器学习的分类

监督学习，训练样本包含对应的“标签”，如识别问题
• 分类问题，样本标签属于两类或多类（离散）
• 回归问题，样本标签包括一个或多个连续变量（连续）
无监督学习，训练样本的属性不包含对应的“标签”，如聚类问题

半监督学习：依赖于部分被标注的数据

强化学习：一种序列数据决策学习方法，一般从环境交互中学习。

回归与分类的区别：回归与分类均是挖掘和学习输入变量和输出变量之间潜在关系模型，基于学习所得模
型将输入变量映射到输出变量

回归输出变量是连续的，分类输出变量是离散的

训练集&测试集：将数据集划分为训练集&测试集，从训练集学到映射函数f，并在测试集测试训练函数的准确性。

4.1.3监督学习

1)标注数据:标识了类别信息的数据

2)学习模型:如何学习得到映射模型

3)损失函数:对学习结果进行度量

损失函数

训练集中一共有𝑛个标注数据，第𝑖个标注数据记为(𝑥𝑖, 𝑦𝑖) ,其中第𝑖个样本数据为𝑥𝑖，𝑦𝑖是𝑥𝑖的标注信息。

从训练数据中学习得到的映射函数记为𝑓， 𝑓对𝑥𝑖的预测结果记为𝑓(𝑥𝑖) 。损失函数就是用来计算𝑥𝑖真实值𝑦𝑖 与预测值𝑓(𝑥𝑖)之间差值的函数。

训练过程中希望映射函数在训练数据集上得到 “损失”之和最小，即

经验风险:训练集中数据产生的损失，经验风险越小说明学习模型对训练数据拟合程度越好。

期望风险:当测试集中存在无穷多数据时产生的损失，期望风险越小，学习所得模型越好。

过拟合（过学习）和欠拟合（欠学习）

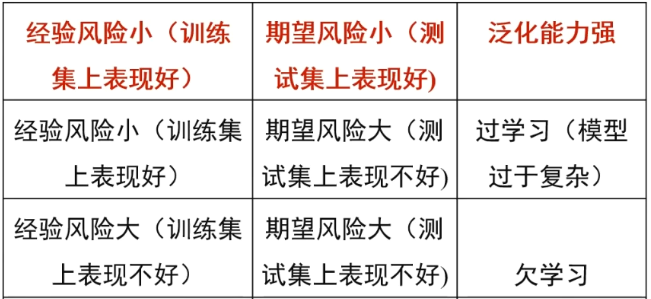
结 构 风 险 最 小 化 ：为了防止过拟合，在经验风险上加上表示模型复杂度的正 则 化 项 或 惩 罚 项：

监督学习两种方法：判别模型与生成模型

python scikit-learn使用流程

4.2线性回归

4.3逻辑回归

线性回归模型（直线）有时难以刻画数据的复杂分布，需要寻找非线性回归模型（曲线）

4.5决策树

决策树是一种监督学习的分类方法，决策树是一种树形结构，其中每个非叶子结点表示对分类目标在某个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果。

建立决策树过程：不断选择属性值对样本集进行划分，直到每个子样本为同一个类别。

贪婪策略：根据优化某些条件的属性测试划分记录。

属性类型 • Nominal（标称） • Ordinal（顺序） • Continuous（连续）

划分方式

（基于标称属性）

• 二元划分 ：将属性值分成两个子集。因此需要找到最优划分的判决方法。

• 多元划分：输出数取决于该属性不同属性值个数。

（基于连续属性）

•离散化以形成有序分类属性

静态划分-算法开始时一次性固定好量化区间

动态划分-范围可以通过等宽法，等频率法，聚类。

• 二元决策: (A < v) or (A≥ v)

考虑所有可能的划分，找到最好的划分 • 可能需要更多的计算

如何确定最佳划分?
• 贪心算法:具有均匀类分布的节点优先（每个子节点数量相似）

节点杂质的度量

1.Gini Index（基尼系数）

基于GINI的拆分

2.基于熵的分割

3.基于INFO的拆分

4.6朴素贝叶斯

P(h)：在没有训练数据前假设h拥有的初始概率（先验概率）

P(D)表示训练数据D的先验概率，P(D|h)表示假设h成立时D的概率

机器学习中，我们关心的是P(h|D)，即给定D时h的成立的概率，（h的后验概率）

极大后验假设

极大似然假设

第5章 聚类

聚类任务：将大量数据根据他们的数据特征相似性分成少量簇的任务。

聚类算法目标：得到一个聚类结果，以最小化类内距离（或最大化类内相似度），而最大化类间距离（或最小化类间相似度）。

5.1 K均值聚类（K-means)

算法要求：特征变量连续，数据没有异常值。

算法目标：找到“局部最优”

伪码

1.初始化聚类质心

初始化K个聚类质心c={c₁,c₂,...c_k},c_j∈R^d(1≤j≤K），每个聚类质心c_j所在集合记为G_j

d是属性，质心是该类所有点的平均值

初始化质心是随意的，所以该算法易受初始值影响很大。

2.对数据进行聚类

将每个聚类数据放入唯一一个聚类集合。

计算每个待聚类数据和K个聚类质心的距离。常用欧氏距离，计算X_i和C_j之间的距离将每个X_i放入与之距离最近的聚类质心所在的聚类集合

3.更新聚类质心

5.2 DBSCAN

DBSCAN(具有噪声的基于密度的聚类方法)是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，它将簇定义为密度相连的点的最大集合。

密度：指定半径内的点数（Eps)

核心点(core point)如果一个点在Eps中的点数超过指定的点数（MinPts）

边界点(border point)在Eps中的点数少于MinPts，但位于核心点附近

伪码