本文随复习进度更新,本文只含重点公式,可能内容不是很全
一、行列式
分块行列式

二、矩阵
逆矩阵
充要条件:|A|≠0
伴随矩阵法: A*=|A|A-1
初等变换![]()
常用性质
矩阵转置 (AB)T=BTAT
伴随矩阵 (A*)T=(AT)* (kA)*=kn-1A* (AB)*=B*A* 若A为方阵 |A*|=|A|n-1(n为A的维度)
逆矩阵 (A-1)T=(AT)-1 若A为方阵 |A-1|=|A|-1
矩阵的秩
m × n 矩阵的秩最大为m和 n的最小值
可逆矩阵满秩(满秩矩阵的行列式≠0)
r(A)=r(AT)=r(ATA)=r(AAT)
r(A±B)≤r(A)+r(B)
r(AB)≤min{r(A),r(B)}
A为m×n矩阵,B为n×s矩阵,且AB=0,则r(A)+r(B)≤n
矩阵左(右)乘可逆矩阵,秩不变
三、向量
基本运算
内积: (a,b)=(b,a)=aTb=bTa (a,a)=|a|2 (a,k1b1+k2b2+...+knbn)=k1(a,b1)+k2(a,b2)+...+kn(a,bn)
正交: (a,b)=0时,a,b正交
向量组的线性相关
相关性:齐次线性方程x1a1+x2a2+...xnan=0 只有零解:线性无关 有非零解:线性相关
线性表示:x1a1+x2a2+...xnan=b 有解:向量b可由向量组a1,a2...,an线性表示
相关性质
1:向量组线性相关的充要条件是向量组中至少存在一个向量可由其余向量线性表示(含0向量的向量组一点线性相关)
2:线性无关的向量组其任何组成部分都线性无关,反之若向量组的部分线性相关的则向量组一定线性相关
3.向量组a1,a2...an线性无关的充要条件是|a1,a2...,an|≠0
4.设a1,a2...,an是n个m维向量,若m<n,则向量组a1,a2...,an一定线性相关
6.设a‘1,a’2...,a‘n是a1,a2...,an的扩充向量组(增加维数),若a1,a2...,an线性无关,则a‘1,a’2...,a‘n线性无关,反之不一定成立。
7.设a1,a2...,an是两两正交的非零向量组,则a1,a2...,an线性无关,反之不一定成立。
向量组的等价、极大线性无关组、秩
向量组等价定义:两个维数相同的向量组可以相互线性表示。
极大线性无关组:向量组a1,a2...,an中存在r个向量线性无关,r+1(也可能不存在)一定线性相关,则r个线性无关的向量组为向量组a1,a2...,an的极大线性无关组,r(极大线性无关组包含的向量个数)为向量组的秩。
秩的性质
线性无关的向量组满秩
矩阵的秩=矩阵的行秩=矩阵的列秩
若向量组A可由向量组B表示,则r(A)≤r(B)(若B不可由A表示,则r(A)<r(B))
等价向量组秩相等,反之不一定成立。
四、线性方程组
3种表示形式
1.基本形式
2.矩阵形式 齐次AX=0 非齐次AX=b
3.向量形式 齐次x1a1+x2a2+..+xnan=0 非齐次x1a1+x2a2+..+xnan=b
定理
基本定理
1. 对齐次线性方程组AX=0,A为m×n矩阵:
只有零解的充要条件:r(A)=n(相当于约束条件=未知数个数,无自由变量);
非零解(无数解)的充要条件:r(A)<n(相当于约束条件<未知数个数,有自由变量,则有无数个解);
(m是约束条件个数,秩相当于“有效约束条件”的个数,n是未知数的数量,n - r(A)表示基础解系向量个数)
2. 对非齐次线性方程组AX=b,A为m×n矩阵,增广矩阵![]() =(A:B):
=(A:B):
有解的充要条件:r(A)=r(![]() ) 其中有唯一解充要条件r(A)=r(
) 其中有唯一解充要条件r(A)=r(![]() )=n,有无数个解充要条件r(A)=r(
)=n,有无数个解充要条件r(A)=r(![]() ) <n
) <n
无解的充要条件:r(A)≠r(![]() )
)
补充定理
解的结构

求解
齐次线性方程
若r(A)<n,则AX=0所有解构成的解向量组的极大线性无关组称为方程组AX=0的一个基础解系(基础解系中所含的线性无关的解向量个数为n-r个。
求解步骤
系数矩阵A→(初等行变换)阶梯化→每行第一个非0元素(一般化为1)所在列对应未知数是约束变量,其余变量是自由变量→基础解系
相当于用自由变量表示约束变量

X3和X4分别取(0,1)和(1,0)即可得基础解系。
相当于约束变量部分直接用通解所在列取反后替代
非齐次线性方程
先令AX=0求出一个基础解系( ξ1, ξ2...ξn-r)
求出AX=b的一个特解η0
则AX=b的通解为 k1ξ1+..+kn-rξn-r+η0
五、特征值&特征向量
基本概念
二次型:未知数的个数是任意多个,且每一项的次数均为2的多项式
A为n阶矩阵,若存在常数λ以及n维非零列向量α,使得Aα=λα,则λ是矩阵A的特征值,α是矩阵A关于λ的特征向量。n阶矩阵一定有n个特征值
特征方程:| λE - A | = 0 为矩阵A的特征方程。
- 同一个特征值对应的特征向量,无论如何线性组合还是特征向量。不同特征值对应的特征向量,线性组合后不是特征向量
矩阵的迹:a11+a22+...+ann
矩阵相似:A、B均为n阶矩阵,若存在可逆矩阵P,使P-1AP=B,则A~B。
性质
- 若A~B,则 |A|=|B| tr(A)=tr(B)
相似对角化:A、B均为n阶矩阵,若存在可逆矩阵P,使P-1AP=∧(∧是对角矩阵)。
施密特正交化:把一组线性无关的向量组转化为两两正交且规范的向量组的过程。
设α1、α2 ... αn线性无关
(1)正交化
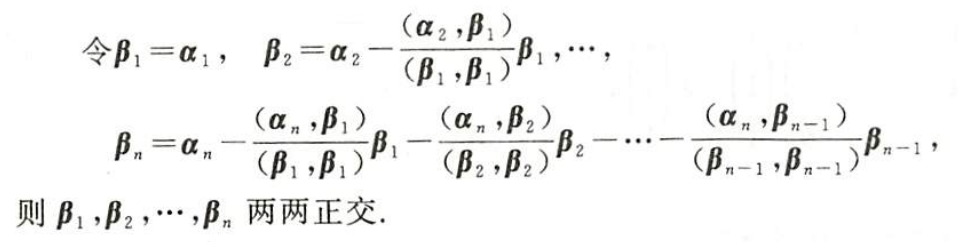
(2)规范化
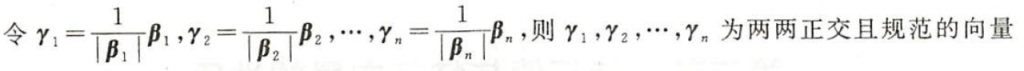
正交矩阵:设Q为n阶矩阵,则QTQ=E(或QQT=E),称Q为正交矩阵。
相关性质
一般性质
定理1:A为n阶矩阵,λ1 , λ2 , ... ,λn是A的特征值,则
λ1+λ2+ ... +λn = tr(A)
λ1λ2 ... λn = |A|
定理2:设A是n阶矩阵,λ0是A的k阶特征值,则
1)若k=1,λ0是单特征值,则属于λ0的线性无关特征向量只有1个
2)若k>1,则属于特征值λ0的线性无关特征向量不超过k个
定理3:A为n阶矩阵,有特征值λ,特征向量α
若A可逆, 1/λ是A-1的特征值,α是A-1的特征向量
若A可逆, |A|/λ是A*的特征值,α是A*的特征向量
f(x)=anxn+ ... +a1x+a0 令 f(A)=anAn+ ... +a1A+a0E , 则有f(λ)是f(A)的特征值, α是f(A)的特征向量
实对称矩阵特征值和特征向量的性质
实对称矩阵A=AT
若A是实对称矩阵,则A的特征值均为实数,不同特征值对应的特征向量正交。
矩阵对角化理论
解题方法
1.求特征值特征向量
公式法 | λE - A | = 0
定义法( AX=λX ) 求 ( λ0E-A)X=0的基础解系得到关于特征值λ0的线性无关的特征向量。
关联矩阵法 若A可逆,则A-1,A*和A特征向量相同
2.矩阵相似的判断
①必要条件:矩阵的秩、行列式、| λE - A | = | λE - B | 、特征值相同
②
1)若A、B均可对角化,则有n个不同特征值或K重特征值有K个线性无关的特征向量(r(λE-A)=n-k)
2)若A、B只有一个可以对角化,则A、B不相似
3)若A、B均不可对角化,则A~B的充要条件r(λiE-A)=r(λiE-B) (i=1,2,3...n)










Comments | 2 条评论
感谢分享,赞一个
非常不错的文章